$V_D$表大DC,$v_D$表全信号,$v_d$表小AC
热电压常数$V_T=\frac{k}{q}T$在常温(27度)默认为26mV
$V_S$域值电压 $V_{TH}$为BJT重要参数
电容&电感
电容
模型
$$
q=CU
$$
$$
i(t)=\frac{dq}{dt}=C\frac{du}{dt}
$$
$$
u_c(t)=\frac{1}{C}\int_{-\infty}^0i(\xi)d\xi+\frac{1}{C}\int^t_0i(\xi)d\xi
$$
电压的记忆性
峰值检测器电路
电压的连续性
电容电流有界时,电压不能突变
储能
$$
p(t)=u(t)C\frac{du}{dt}
$$
$$
W(t_0,t)=\int_{t_0}^tp(\xi)d\xi=\frac{1}{2}C[u^2(t)-u^2(t_0)]
$$
若初始储能为0,则任意时刻能量:
$$
W(t)=\frac{1}{2}Cu^2(t)
$$
某时刻电容储能只取决于电压,与电流无关
串并联
并联变大,串联变小
电感
模型
$$
\psi =Li
$$
$$
u(t)=\frac{d\psi}{dt}=L\frac{di}{dt}
$$
$$
i(t)=\frac{1}{L}\int_{-\infty}^0u(\xi)d\xi+\frac{1}{L}\int_0^tu(\xi)d\xi
$$
电流的记忆性
电流的连续性
储能
$$
p(t)=i(t)L\frac{di}{dt}
$$
$$
w(t_0,t)=\frac{1}{2}L[i^2(t)-i^2(t_0)]
$$
某时刻电容储能只取决于电流,与电感无关
串并联
并联变小,串联变大
一阶电路的暂态过程
全响应-三要素法(仅限直流激励一阶)
$$
f(t)=[f(0_+)-f(\infty)]e^{-\frac{t}{\tau}}+f(\infty)\space (t\geq0)
$$
全响应 = 固有响应(瞬态响应) + 强制响应(稳态响应)
注意:非直流激励下,固有响应不等于瞬态响应,稳态响应不等于稳态响应
瞬态响应:随t变化 固有响应:由内部电路原本状态引起的变化
$$
f(t)=f(0_+)e^{-\frac{t}{\tau}}+f(\infty)(1-e^{-\frac{t}{\tau}})\space(t\geq 0)
$$
全响应 = 零输入响应 + 零状态响应
$$
\tau=R_0C\space or\space\tau=\frac{L}{R_0}
$$
$\tau$ 具有时间但量纲,称为RC电路的时间常数
一般用$3\tau$ 法判断放电过程结束,即90%
计算R时,电容用戴维宁等效,电感用诺顿等效
:warning:注意
电容电路里,电流可以跃变;电感电路里,电压可以跃变
注意表达式范围是否包含0
包含开关序列的直流一阶电路
阶跃函数
$$
\varepsilon(t)=\begin{cases}
0 & t<0\\
1 & t>0
\end{cases}
$$
引入阶跃电流源和阶跃电压源可以省去电路中的开关,可以应用叠加定理计算电路的零状态响应
阶跃响应
单位阶跃信号作用下电路的零状态响应,用$s(t)$表示
已知电路的阶跃响应,利用叠加定理易得任意分段恒定信号激励下线性时不变电路的零状态响应
冲激函数
一个无界信号$\delta(t)$为单位冲激函数当且仅当
$$
\begin{cases}
\delta(t)=\begin{cases}
奇异值&t=0\\
0&t\neq 0
\end{cases}\\
\int_{-\varepsilon_2}^{\varepsilon_1}\delta(t)dt=1&\varepsilon_1>0,\varepsilon_2>0
\end{cases}
$$
单位阶跃函数与单位冲激函数间存在关系
$$
\delta(t)=\frac{d\varepsilon(t)}{dt}
$$
$$
\varepsilon(t)=\int^t_{-\infty}\delta(\xi)d\xi
$$
冲激响应
单位冲激信号作用下电路的零状态响应,表示为$h(t)$
可先求出$s(t)$,对时间求导
二阶电路的暂态过程
仅讨论含两个动态原件的线性二阶电路
RLC串联电路的零输入响应
常系数非齐次线性二阶微分方程:
$$
LC\frac{d^2u_c}{dt^2}+RC\frac{du_c}{dt}+u_c=u_s(t)
$$
电路微分方程的特征根(电路的固有频率):
$$
s_{1,2}=-\frac{R}{2L}\pm\sqrt{(\frac{R}{2L})^2-\frac{1}{LC}}
$$
- $R>2\sqrt{\frac{L}{C}}$ ,$s_{1,2}$为不相等实根,过阻尼情况
- $R=2\sqrt{\frac{L}{C}}$ ,$s_{1,2}$为相等实根,临界阻尼情况
- $R<2\sqrt{\frac{L}{C}}$ ,$s_{1,2}$共轭复数根,欠阻尼情况
对R来说,越大越不易震荡,R趋近$\infty$时开路;越小越易震荡,R为0时为LC震荡电路
L越大(L储能越大,$\frac{1}{2}L\Delta i^2$大,电流变化大)C越小($q=CU$电压变化越大),越容易震荡
过阻尼
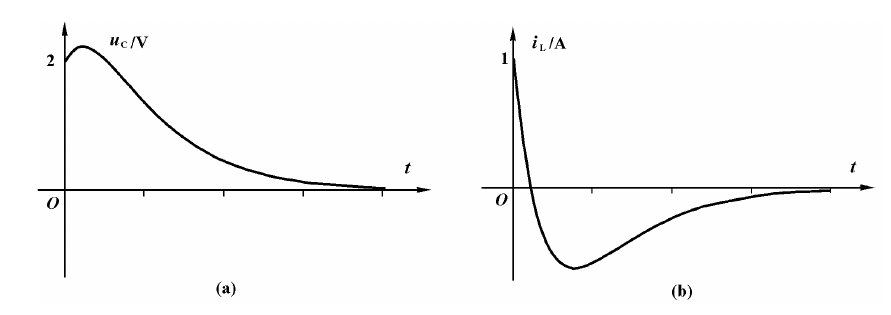
临界阻尼
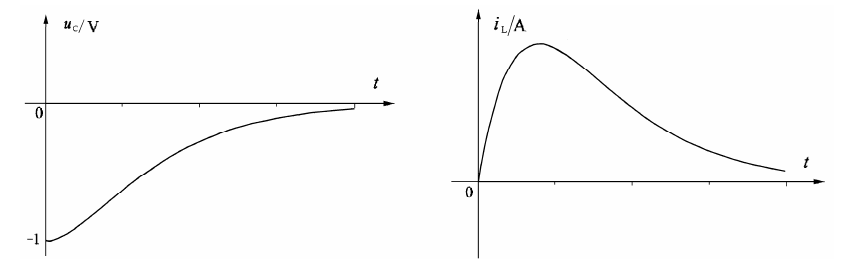
欠阻尼
$$
s_{1,2}=-\frac{R}{2L}\pm\sqrt{(\frac{R}{2L})^2-\frac{1}{LC}}=-\alpha\pm j\sqrt{w_0^2-\alpha^2}=-\alpha\pm jw_d
$$
衰减因子$\alpha=\frac{R}{2L}$,因为RCL串联电路震荡快慢由i决定,故用电感时间常数,等于$\frac{1}{2\tau}$
无阻尼自然(谐振)频率$w_0=\frac{1}{\sqrt{LC}}$
有阻尼自然频率$w_d=\sqrt{w_0^2-\alpha^2}$
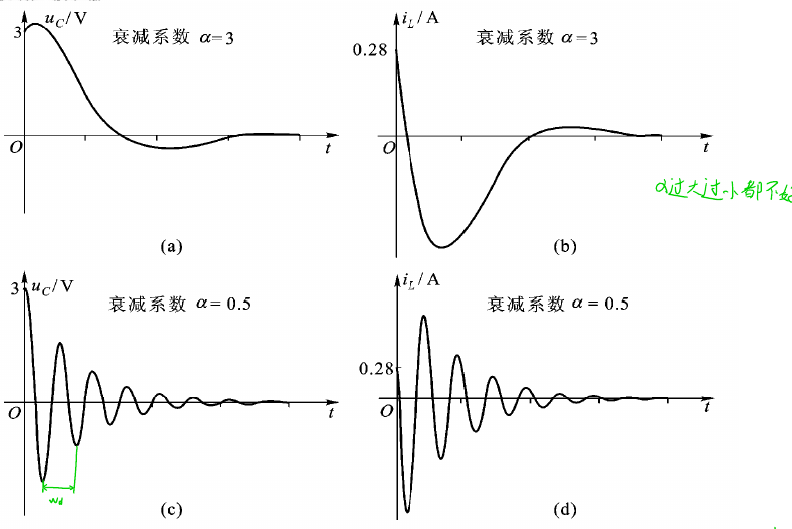
欠阻尼能量在电容与电感之间交换
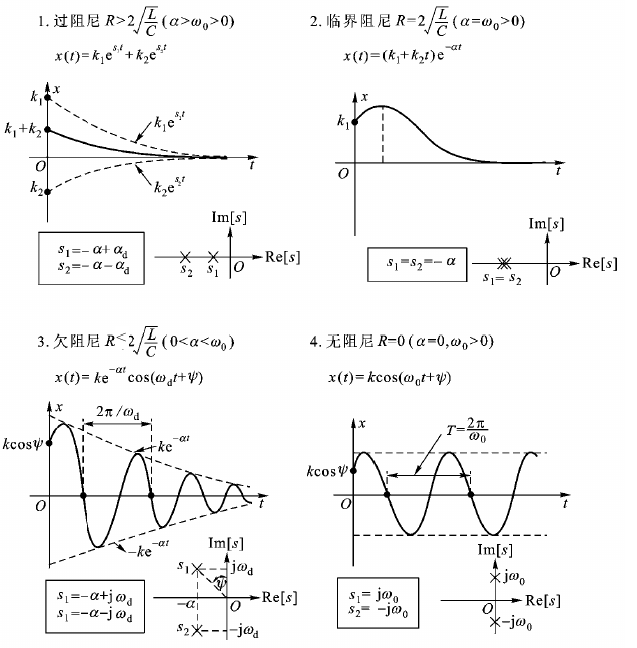
直流激励下RLC串联电路的响应
全响应由对应齐次微分方程通解与微分方程特解之和组成
$$
u_c(t)=u_{Ch}(t)+u_{Cp}(t)
$$
$s_1\neq s_2$时
$$
u_c(t)=K_1e^{s_1t}+K_2e^{s_2t}+U_S
$$
利用
$$
u_c(0),\frac{du_c(t)}{dt}\Bigg |_{t=0}=\frac{i_L(0)}{C}
$$
求解$K_1K_2$
RLC并联电路的零输入响应
$$
LC\frac{d^2i_L}{dt^2}+GL\frac{di_L}{dt}+i_L=i_s(t)
$$
$$
s_{1,2}=-\frac{R}{2L}\pm\sqrt{(\frac{R}{2L})^2-\frac{1}{LC}}
$$
$$
s_{1,2}=-\frac{G}{2C}\pm\sqrt{(\frac{G}{2C})^2-\frac{1}{LC}}=-\alpha\pm j\sqrt{w_0^2-\alpha^2}=-\alpha\pm jw_d
$$
衰减因子$\alpha=\frac{G}{2C}$,因为RCL并联电路震荡快慢由u决定,故用电容时间常数,等于$\frac{1}{2\tau}$
无阻尼自然(谐振)频率$w_0=\frac{1}{\sqrt{LC}}$
有阻尼自然频率$w_d=\sqrt{w_0^2-\alpha^2}$